אלגברה בוליאית. חלק 2. חוקים ותפקודים בסיסיים

המשך הסיפור על אלגברה בוליטית, מוסכמות, כללים, פעולות. מעבר ליסודות של מעגלי קשר.

בתוך מאמר ראשון ג'ורג 'בול תואר כיוצר האלגברה של ההיגיון. המאמר השני יתאר את הפעולות הבסיסיות של אלגברה בוליאנית, ושיטות לפשט ביטויים בוליאניים. אם כן, האלגברה הבוליתית משתמשת בהצהרות כטיעונים, ולא כמשמעותם, אלא באמת או בכזב של ההצהרה.

הטופס לכתיבת ביטויים באלגברה בוליאית.

אם ההצהרה נכונה, אז זה כתוב כך: A = 1, אם הוא שקרי, אז A = 0 (אחרי הכל, זה לא נכון שתפוח אדמה הוא פרי). עבור כל הצהרה, A הוא נכון (A = 1) או שקר (A = 0). לא יכול להיות כאן אמצע. כבר דיברנו על זה.

אם אתה מחבר שתי הצהרות פשוטות עם האיחוד וכן, אתה מקבל הצהרה מורכבת, המכונה מוצר הגיוני. בואו ניקח שתי הצהרות פשוטות: "שלוש זה יותר משני" נקבע באות A, "שלוש פחות מחמש" - לפי אות ב.

מכאן שהאמירה המורכבת "שלוש היא יותר משניים ופחות מחמישה" היא הגיונית (במקרה זה, אות ההון אני מציינת שמדובר בפעולה לוגית "וגם", וכן בהמשך הטקסט "או" ו- "לא.") ו- B. זה מוגדר כך: A ^ B או A * B.

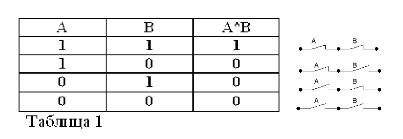
כפל לוגי (פעולה "AND").

באלגברה אלמנטרית A * A = A2. אבל באלגברה של בוהל A * A = A2 = A, A * A = A, מכיוון שסימן הכפל (*) פירושו עכשיו ... ו ... במובן של And ... ו-. כל הניסיון שלנו מאשר כי A&A זהה ל- A. בלבד. אי אפשר להסכים עם זה. האמת של ההצהרה אינה משתנה אם היא חוזרת על ידי הגורם מספר פעמים.

תוצר של שתי הצהרות נחשב נכון (שווה ל -1), אם כן, ורק אם שני הגורמים הם נכונים, ושקריים (שווה ל 0) אם לפחות אחד הגורמים הוא שקרי. מסכים כי כללים אלה אינם עומדים בסתירה לשכל הישר, ובנוסף, הם עומדים לחלוטין בכללי האלגברה היסודית:

1*1 = 1, 1*0 = 0 = 0*1 = 0, 0*0 = 0.

השוויון הראשון נקרא כך: אם גם A וגם B הם נכונים, אז המוצר A * B הוא נכון. באלגברה של בוהל, סימן הכפל (*) מחליף את האיחוד הראשון.

מוצרים לוגיים עשויים לכלול לא שניים, אלא מספר גדול יותר של הצהרות - גורמים. ובמקרה זה, המוצר נכון רק כאשר יחד עם זאת כל ההצהרות-גורמים נכונים.

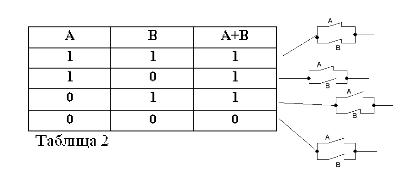
תוספת לוגית (פעולה OR)

אם שתי הצהרות קשורות על ידי איחוד או. המשפט המורכב שנקרא נקרא סכום הגיוני.

קחו דוגמה לסכום הגיוני. באומר א ': "היום אני אלך לקולנוע."

הצהרה ב ': "היום אני אלך לדיסקו." אנו מוסיפים את שתי האמירות ומקבלים: "היום אני אלך לקולנוע או לדיסקו."

אמירה מורכבת זו מציינת כך: A + B = C או (A V B) = C.

על ידי C ציינו אמירה מורכבת של סכום הגיוני.

בדוגמה הנדונה לא ניתן להשתמש באיחוד OR במובן בלעדי. אכן, באותו יום תוכלו להגיע לקולנוע ולדיסקו. והנה האמרה:

"יו"ר השותפות בגינון יהיה פטרוב או איבנוב," הוא לא סכום הגיוני, מכיוון שרק אדם אחד יהיה היו"ר, והשני יהיה גנן רגיל חובב.

הסימן V לסכום הלוגי נבחר מכיוון שהוא האות הראשונית של המילה הלטינית "vel", שמשמעותה "או", בניגוד למילה הלטינית "aut> שמשמעותה" ו- ". כעת צריך להיות ברור לכולם מדוע המוצר ההגיוני מסומן על ידי השלט ^.

באלגברה אלמנטרית יש כלל A + A = 2A. כלל זה נכון, לא משנה איזה מספר מיוצג על ידי האות A. באלגברה הבוליאנית, הכלל A + A = A תואם את זה. כל חווית חיינו אומרת שאומר A או A או שניהם A זה פשוט דרך אחרת וארוכה יותר לומר רק A.

כמו כל הצהרה מורכבת, סכום שתי ההצהרות A ו- B יכול להיות אמיתי או כוזב. הסכום נחשב נכון, כלומר שווה לאחדות, אם לפחות אחד מהתנאים נכון:

A + B = 1 אם OR A = 1 או B = 1, התואם את החשבון המקובל:

1+0 = 0+1 = 1.

אם שתי האמירות המסוכמות נכונות, הסכום נחשב גם לאמת, לכן באלגברה הבולאנית יש לנו: (1) + (1) = 1.

הסוגריים מוגדרים כאן בכדי להדגיש את התנאי, את המשמעות של תוספת זו ולא את החשבון.

סכום של שתי הצהרות נחשב ככזה ושווה לאפס אם, אך רק אם שני המונחים שגויים. מכאן:

0 + 0=0.

אז סכום שתי ההצהרות A + B נחשב נכון אם נכון, OR A, OR B, OR שניהם מונחים זה בזה. לפיכך, המילה OR מסומנת על ידי +.

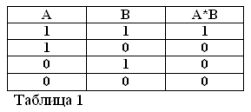
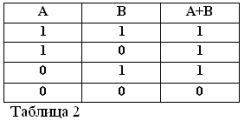
כזכור, כי הצהרות A ו- B יכולות להיות נכונות או כוזבות בלבד, ולכן יש מידה לאמת 1 או 0, ניתן לסכם את תוצאות הפעולות ה– AND ו- OR בטבלאות 1 ו- 2.

הפעולה השלישית, בשימוש נרחב על ידי אלגברה של בוהל, היא פעולת השלילה - לא. אנו מזכירים לכם כי אלגברה אלמנטרית משתמשת בפעולות הוספה, חיסור D, הכפל על ידי, חלוקה על ידי וכמה אחרים.

לכל הצהרה א 'יש השלילה שלה לא A, אותה נציין בסמל / א. זה לא אמור להיות בספק.

אנו נותנים דוגמאות: "נלך ליער" א, "לא נלך ליער" / א.

אם האמירה A נכונה, כלומר A = 1, אז שלילתה / A חייבת להיות שקרית / A = 0. ולהיפך, אם כל הצהרה שגויה, אז השלילה שלה נכונה. לדוגמא: "סוס לא אוכל חציר" / A = 0, "סוס לא אוכל חציר" (A = 1). ניתן לבטא זאת בטבלה 3.

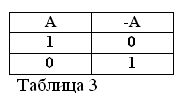
קביעת המשמעות של פעולת השלילה, ובהנחה כי משתי ההצהרות A ו- / A היא תמיד אמת אחת, שתי הנוסחאות החדשות של האלגברה הבולאנית עוקבות אחר כך:

A + (/ A) = 1 ו- A * (/ A) = 0.

ישנן נוסחאות נוספות שמפשטות את העיבוד ההגיוני של הצהרות. לדוגמא, 1 + A = 1, מכיוון שעל פי הגדרת התוספת, במקרה בו מונח אחד שווה לאחדות, הסכום שווה תמיד לאחדות. התוצאה המתקבלת אינה תלויה אם A = 0 או A = 1.

לכל אחת משלוש הפעולות הלוגיות שבדקנו (AND, OR, NOT) יש תכונות מסוימות שקרובות לכללי האלגברה האלמנטרית. אם כולם מנוסחים, נקבל 25 כללים של אלגברה בוליטית. הם די מספיקים כדי לפתור כמעט כל בעיה הגיונית. ללא כללים אלה, קשה למדי לפתור בעיות לוגיות בגלל המורכבות הנראית לעין. ניסיון למצוא את התשובה הנכונה מבלי להשתמש בכללים פירושו להחליף אותם בכושר ההמצאה וההנמקה הכללית. כללים מקלים מאוד על עבודה זו וחוסכים זמן.

במסגרת המאמר, אי אפשר לקחת בחשבון את כל 25 הכללים הללו, אך מי שרוצה יוכל למצוא אותם תמיד בספרות הרלוונטית.

כפי שכבר הוזכר במאמר הראשון בשנת 1938, המדען האמריקני הצעיר קלוד שאנון במאמרו "ניתוח סמלי של מעגלי ממסר ומתגים" משתמש לראשונה באלגברה בוליטית לבעיות של טכנולוגיית ממסר. התגלית של שאנון הייתה שהוא הבין שהשיטה לעיצוב מכונות ממסר ומחשבים אלקטרוניים היא למעשה ענף של היגיון מתמטי.

זה קורה לעתים קרובות. במשך שנים רבות המדען עובד על בעיה שנראית מיותרת לחלוטין עבור בני ארצו - פשוט כיף. אך עשרות שנים ולפעמים מאות עוברות, ותאוריה שאיש אינו זקוק לה אינה רק רוכשת את זכות הקיום, אלא שבלעדיה התקדמות נוספת הופכת בלתי נתפסת.

מה עזר לשאנון בפעם השנייה "לגלות" את האלגברה הבוליאנית? מקרה? שום דבר מהסוג.

האהבה למכונות ממסר, הבנויה על מתגים וממסרים קונבנציונליים, עזרה למדען הצעיר לחבר תיאוריה שנשכחה למשימות של חילופי טלפון אוטומטיים, עליהם עבד באותה תקופה. מאוחר יותר, שאנון הכניס את אותו רעיון של "כן או לא" למסרים נפרדים והניח את הבסיס לקטע שלם בסייברנטיקה - תורת המידע.

האלגברה של בוהל התאימה מאוד לניתוח וסינתזה של מעגלי ממסר. די היה בכדי לקבל הצהרה אמיתית: "יש איתות במעגל", וכאמור כוזב - "אין איתות במעגל", כפי שהופיעה אלגברה חדשה - אלגברה האות, אלגברה של מעגל הממסרים.

האלגברה החדשה תקפה רק לשיקול מעגלי ממסר ומיתוג. אחרי הכל, רק בסכמות כאלה מתקיים התנאי "יש איתות" ו"אין איתות ". כאשר האות משתנה ברציפות, ורכישת מספר גדול באופן שרירותי של תנאי ביניים (אות כזה נקרא אנלוגי), אלגברה ממסר אינה חלה. תמיד צריך לזכור את זה. אך רק רוב המחשבים האלקטרוניים והמכונות הסייברנטיים משתמשים בעיקרון הבודד של עיבוד אותות, המבוסס על האלמנטים "כן - לא".

הביטוי "איש קשר נסגר" התקבל על ידי שאנון כנכון (1), ו"יש קשר פתוח "כשקר (0). שאר ה"אלגברה ", כולל פעולות AND, OR ו- NOT ו- 25 כללים, שאנון שאיל מבולה.

אלגברה של מעגלי הממסרים התבררה כפשוטה יותר מאלגברה הבוליאנית, מכיוון שהיא עוסקת רק באלמנטים מסוג "כן - לא". בנוסף, האלגברה החדשה חזותית יותר.

האלמנטים באלגברה זו הם אנשי הקשר, אותם נציין באמצעות האותיות A, B, C ... איש הקשר סגור - A, איש הקשר פתוח - / A (אות עם מקף).

הסימן, כפי שאתה רואה, לקוח לחלוטין מאלגברה בוליטית. איש קשר פתוח הוא שלילה של קשר סגור. אותו איש קשר לא יכול להיות סגור ופתוח גם יחד.

בואו נסכים שאם במעגל כלשהו שני אנשי קשר מציינים אותו אות זה אומר שהם תמיד לוקחים את אותם הערכים.

בכל רגע נתון, שניהם פתוחים בו זמנית, או שניהם סגורים. הדרך הקלה ביותר לדמיין אותם מחוברים זה לזה באופן מכני כך ששניהם נפתחים או סוגרים בו זמנית.

אם בשרשרת כלשהי איש קשר הוא שלילה של קשר אחר, אז המשמעות שלהם תמיד הפוכה. לדוגמה, אנשי קשר C ו / C לעולם לא יכולים להיות פתוחים בו זמנית או להיסגר בו זמנית. ובתרשים אפשר לייצג אותם מחוברים מכנית: אם אחד מהם נפתח, השני נסגר.

אנו מתחילים את היכרותנו עם אלגברה ממסרים על ידי ניתוח המעגלים הפשוטים ביותר התואמים לפעולות AND, OR ו- NOT.

תוצר של שני אנשי קשר (פעולה AND) הוא המעגל המתקבל כתוצאה מחיבור הסדרה שלהם: הוא סגור (שווה ל 1) רק כאשר שני המגעים סגורים (שווה ל 1).

סכום שני המגעים (פעולה OR) יהיה המעגל שנוצר כאשר הם מחוברים במקביל: הוא סגור (שווה ל 1) כאשר לפחות אחד מהמגעים היוצרים את המעגל סגור (שווה ל 1).

ההפך ממגע זה (פעולה לא) הוא מגע השווה ל 0 (פתוח) אם איש קשר זה הוא 1 (סגור), ולהיפך.

כמו באלגברה הבולאנית, אם המגעים מסומנים על ידי האותיות A ו- B, אנו נציין את התוצר של שני אנשי קשר על ידי A * B, את הסכום על ידי A + B, ואת המגע שממול A, על ידי / A. האמור לעיל מוסבר באיורים 1, 2 ו -3.

תוקף של טבלאות המתאימות לפעולות AND, OR ו- NOT. עכשיו אף אחד לא צריך להיות בספק.

בואו להתעכב על שתי דוגמאות: 1 * 0 = 0 ו- 1 + 0 = 1.

מן הדמות ניתן לראות כי קשר סגור לצמיתות המחובר בסדרה עם מגע פתוח לצמיתות שווה למגע פתוח לצמיתות (1 * 0 = 0) קשר סגור לצמיתות המחובר במקביל למגע פתוח לצמיתות שווה למגע סגור לצמיתות.

לאחר היכרות עם האריתמטיקה של מעגלי מגע, תוכלו לתאר כל מעגל ממסר עם נוסחה באמצעות המוסכמות המקובלות. בסייברנטיקה נוסחאות כאלה נקראות מבניות.

אם הנוסחה המבנית של מעגל ממסר כלשהו היא 1, אז יכול לעבור אות זה - המעגל סגור. לעומת זאת, אם הנוסחה המבנית של המעגל היא 0, האות לא יעבור דרכו - המעגל נשבר.מסקנה: שני מעגלי ממסר שקולים זה לזה כאשר הנוסחאות המבניות שלהם שוות.

בהמשך המאמר, נשקול דוגמאות למעגלי מגע, מעגלי מגע טיפוסיים ושקוליהם, כמו גם לציור תרשימים לפי נוסחאות מבניות. אנו שוקלים גם את מעגלי ההיגיון העיקריים שמבצעים את הפונקציות של האלגברה הבולית.

המשך המאמר: אלגברה בוליאית. חלק 3. תוכניות יצירת קשר

בוריס אלאדישקין

Comments

[#1 אלכס]

תודה

רק נקודה אחת, פסקה:

"כמו באלגברה הבולאנית, אם המגעים מסומנים על ידי האותיות A ו- B, אנו נציין את התוצר של שני אנשי קשר על ידי A * B, את הסכום על ידי A + B, ואת המגע שממול A, על ידי / A. האמור לעיל מוסבר באיורים 1, 2 ו -3 ..."

איפה איור 3?