קטגוריות: אלקטרוניקה מעשית, חשמלאים מתחילים
מספר צפיות: 77535
הערות לכתבה: 1
שבבי היגיון. חלק ב '- שערים
 אלמנטים לוגיים פועלים כאלמנטים עצמאיים בצורה של מעגלי מיקרו בדרגת אינטגרציה קטנה והם נכללים כרכיבים במעגלי מיקרו בדרגת אינטגרציה גבוהה יותר. ניתן למנות אלמנטים כאלה יותר מתריסר.
אלמנטים לוגיים פועלים כאלמנטים עצמאיים בצורה של מעגלי מיקרו בדרגת אינטגרציה קטנה והם נכללים כרכיבים במעגלי מיקרו בדרגת אינטגרציה גבוהה יותר. ניתן למנות אלמנטים כאלה יותר מתריסר.
אבל ראשית, נדבר רק על ארבעה מהם - אלה האלמנטים AND, OR, NOT ו- NOT. האלמנטים העיקריים הם שלושת הראשונים, ואלמנט AND-NOT הוא כבר שילוב של אלמנטים AND AND NOT. ניתן לכנות אלמנטים אלה "לבנים" של הטכנולוגיה הדיגיטלית. ראשית עליכם לקחת בחשבון מה ההגיון בפעולה שלהם?
נזכיר את החלק הראשון של המאמר על מעגלים דיגיטליים. נאמר שהמתח בכניסה (פלט) של המיקרו מעגל בתוך 0 ... 0.4 V הוא רמת אפס היגיון, או רמת מתח נמוכה. אם המתח הוא בתוך 2.4 ... 5.0 וולט, זה הרמה של יחידה לוגית או מתח ברמה גבוהה.
מצב הפעולה של מעגלי מיקרו מסדרת K155 ומעגלי מיקרו אחרים עם מתח אספקה 5V מאופיין ברמות כאלה בדיוק. אם המתח ביציאת המיקרו-מעגל הוא בטווח 0.4 ... 2.4V (לדוגמה, 1.5 או 2.0V), אז כבר תוכלו לחשוב על החלפת מיקרו-מעגל זה.
עצה מעשית: כדי לוודא שמיקרו-מעגל זה לקוי בפלט, עליכם לנתק ממנו את כניסת המיקרו-מעגל העוקב אחריו (או מספר כניסות המחוברות לפלט של מעגל-מעגל זה). כניסות אלה יכולות פשוט "להושיב" (להעמיס יתר) על שבב הפלט.
מוסכמות גרפיות
סמלים גרפיים הם מלבן המכיל שורות קלט ופלט. קווי קלט של אלמנטים ממוקמים משמאל וקווי פלט מימין. כך גם לגבי גיליונות שלמים עם מעגלים: בצד שמאל כל האותות נכנסים, מימין הם פלטים. זה כמו שורה בספר - משמאל לימין, יהיה קל יותר לזכור. בתוך המלבן נמצא סמל מותנה המציין את הפונקציה שמבצע האלמנט.
אלמנט לוגי ו
אנו מתחילים בשיקול של אלמנטים לוגיים עם יסוד I.
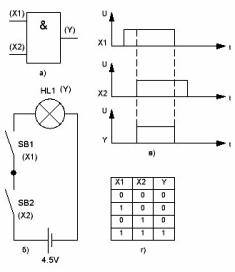
איור 1. האלמנט הלוגי AND
ייעודו הגרפי מוצג באיור 1 א. הסמל של פונקציית ה- And הוא הסמל האנגלי "&", שבאנגלית מחליף את האיחוד "ו-", כי אחרי הכל, כל "הפסאודו-מדע" הזה הומצא בבורגנות הארורה.
כניסות היסוד מוגדרות כ- X עם מדדים 1 ו -2, והפלט, כפונקציית פלט, על ידי האות Y. זה פשוט, כמו במתמטיקה בבית הספר, למשל, Y = K * X או, במקרה הכללי, Y = f (x). לאלמנט יכולים להיות יותר משתי כניסות, אשר מוגבלת רק על ידי המורכבות של הבעיה הנפתרת, אך יכולה להיות פלט אחד בלבד.
ההיגיון של האלמנט הוא כדלקמן: מתח ברמה גבוהה ביציאה Y יהיה רק כאשר ובכניסה X1 ובכניסה X2 יהיה מתח ברמה גבוהה. אם לאלמנט יש כניסות של 4 או 8, אז יש לספק את התנאים המצוינים (ברמה הגבוהה) בכל הכניסות: קלט I-1, קלט I-2, קלט I-כניסה 3 ... .. וכניסה N בלבד. במקרה זה, התפוקה תהיה גם גבוהה.
על מנת להקל על הבנת ההיגיון בפעולת האלמנט And, האנלוגי שלו בצורת מעגל מגע מוצג באיור 1b. כאן, הפלט של האלמנט Y מיוצג על ידי המנורה HL1. אם המנורה דולקת, אז זה מתאים לרמה גבוהה בפלט של אלמנט I. לעתים קרובות אלמנטים כאלה נקראים 2-I, 3-I, 4-I, 8-I. הספרה הראשונה מציינת את מספר התשומות.
כאותות כניסה X1 ו- X2, משתמשים בלחצני "פעמון" רגילים ללא תיקון. המצב הפתוח של הכפתורים הוא מצב ברמה נמוכה, והמצב הסגור הוא טבעי באופן טבעי. כמקור כוח, התרשים מציג סוללה גלוונית. בעוד הכפתורים במצב פתוח, המנורה כמובן אינה מאירה. המנורה נדלקת רק כאשר לחץ על שני הכפתורים בבת אחת, כלומר I-SB1, I-SB2.כזה הוא הקשר ההגיוני בין אות הכניסה לפלט של האלמנט I.
ניתן לקבל ייצוג חזותי של פעולת האלמנט AND על ידי התבוננות בתרשים הזמן המוצג באיור 1 ג. בהתחלה מופיע אות ברמה גבוהה בכניסה X1, אך דבר לא קרה בפלט Y, עדיין ישנו אות ברמה נמוכה. בכניסה X2, האות מופיע בעיכוב מסוים ביחס לכניסה הראשונה, ובאות פלט Y מופיע אות ברמה גבוהה.
כאשר האות בכניסה X1 נמוך, הפלט מוגדר גם נמוך. לחלופין, במילים אחרות: אות ברמה גבוהה מוחזק ביציאה כל עוד ישנם אותות ברמה גבוהה בשתי הכניסות. ניתן לומר את אותו הדבר לגבי האלמנטים המרובי-קלטיים של I: אם זה 8-I, אז כדי לקבל רמה גבוהה בפלט, יש להחזיק את הרמה הגבוהה בכל שמונה התשומות בבת אחת.
לרוב בספרות הייחוס, מצב הפלט של אלמנטים לוגיים בהתאם לאותות הקלט ניתן בצורה של טבלאות אמת. עבור האלמנט הנחשב 2-I, טבלת האמת מוצגת באיור 1 ד.
הטבלה דומה במקצת לטבלת הכפל, רק קטנה יותר. אם תלמד אותו בזהירות, תבחין שרמה גבוהה בפלט תהיה רק כאשר מתח ברמה גבוהה או, מה אותו דבר, יחידה הגיונית קיימת בשתי התשומות. אגב, ההשוואה של טבלת האמת לטבלת הכפל רחוקה מלהיות מקרית: כל טבלאות האמת האלקטרוניקה יודעות, כאמור, בעל פה.
כמו כן, את הפונקציה וניתן לתאר באמצעות אלגברה של היגיון או אלגברה בוליאית. עבור אלמנט דו-קלט, הנוסחה תיראה כך: Y = X1 * X2 או צורת כתיבה אחרת Y = X1 ^ X2.
אלמנט לוגי OR
בשלב הבא נראה את שער OR.
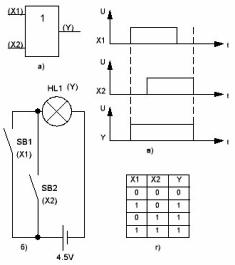
איור 2. איור 2. שער לוגיקה OR
ייעודו הגרפי דומה לאלמנט AND שנבדק זה עתה, אלא שבמקום הסמל & עבור הפונקציה AND, המספר 1 רשום בתוך המלבן, כפי שמוצג באיור 2 א. במקרה זה, הוא מציין את הפונקציה OR. משמאל הם הכניסות X1 ו- X2, שכמו במקרה של הפונקציה And, יכולות להיות יותר, ובימין הפלט, המצוין על ידי האות Y.
בצורה של נוסחת אלגברה בוליטית, פונקציית ה OR כתובה כ- Y = X1 + X2.
על פי נוסחה זו, Y יהיה נכון כאשר OR בכניסה X1, OR בכניסה X2, OR בשתי הכניסות תהיה מיד רמה גבוהה.
דיאגרמת המגע המוצגת באיור 2b תעזור להבין את מה שנאמר זה עתה: לחיצה על אחד מהכפתורים (ברמה גבוהה) או על שני הכפתורים בבת אחת תגרום למנורה לזוהר (ברמה גבוהה). במקרה זה הכפתורים הם אותות הקלט X1 ו- X2, והאור הוא אות הפלט Y. בכדי להקל על הזיכרון, איורים 2c ו- 2d מראים את תרשים התזמון ואת טבלת האמת, בהתאמה: זה מספיק כדי לנתח את פעולת מעגל הקשר המוצג עם התרשים והטבלה, כמו כל השאלות ייעלם.
אלמנט לוגי לא, מהפך
כמו שאמר מורה אחד, בטכנולוגיה דיגיטלית אין דבר יותר מסובך מאשר מהפך. אולי זה למעשה.
באלגברה של ההיגיון, הפעולה אינה נקראת היפוך, שפירושו שלילה באנגלית, כלומר רמת האות בפלט תואמת בדיוק את ההפך לאות הקלט, שנראה כמו Y = / X בצורה של נוסחה
(הקליעה שלפני X מציינת את ההיפוך בפועל. בדרך כלל משתמשים בקו תחתון במקום קו נטוי, אם כי סימון כזה מקובל למדי.)
הסמל הגרפי של האלמנט אינו ריבוע או מלבן שבתוכו רשום המספר 1.
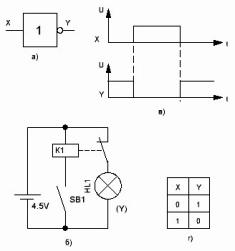
איור 3. מהפך
במקרה זה, המשמעות היא שאלמנט זה הוא מהפך. יש לו רק קלט אחד X ופלט Y. קו הפלט מתחיל במעגל קטן, מה שמצביע למעשה על כך שאלמנט זה הוא מהפך.
כאמור, מהפך הוא המעגל הדיגיטלי המורכב ביותר.וזה מאושר על ידי תכנית הקשר שלו: אם לפני כן היו מספיקים רק כפתורים, כעת נוסף להם ממסר. בזמן שלא נלחץ על כפתור SB1 (אפס לוגי בכניסה), ממסר K1 מופעל ממגע ואנשי הקשר הסגורים שלו בדרך כלל מדליקים את נורית HL1, שתואמת יחידה לוגית ביציאה.
אם תלחץ על הכפתור (החל יחידה לוגית על הקלט), הממסר נדלק, אנשי הקשר K1.1 ייפתחו, האור ייכבה, שתואם לאפס לוגי ביציאה. האמור לעיל אושר על ידי תרשים הזמן באיור 3 ג וטבלת האמת באיור 3d.
אלמנט לוגי ולא
שער AND אינו שילוב של שער AND ושער NOT.
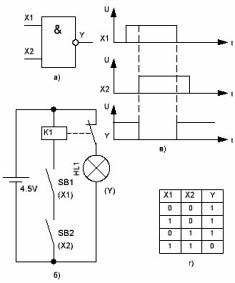
איור 4. האלמנט הלוגי ולא
לכן הסמל & (הגיוני ו- AND) קיים על הסמל הגרפי שלו, ושורת היציאה מתחילה במעגל המציין נוכחות של מהפך בהרכב.
אנלוגי המגע של אלמנט ההיגיון מוצג באיור 4b, ואם מסתכלים מקרוב הוא דומה מאוד לאנלוגי של המהפך שמוצג באיור 3b: הנורה מופעלת גם דרך אנשי קשר סגורים בדרך כלל של ממסר K1. למעשה זהו המהפך. הממסר נשלט על ידי הכפתורים SB1 ו- SB2, התואמים את הכניסות X1 ו- X2 של שער AND. התרשים מראה שהממסר יופעל רק כאשר נלחצים על שני הכפתורים: במקרה זה הכפתורים מבצעים את הפונקציה & (לוגית AND). במקרה זה, המנורה בפלט נכבה, שתואמת למצב של אפס לוגי.
אם לא נלחצים על שני הכפתורים, או לפחות על אחד מהם, אזי הממסר מושבת, והאור ביציאת המעגל דולק, התואם לרמה של יחידה לוגית.
מהאמור לעיל, ניתן להסיק את המסקנות הבאות:
ראשית, אם לפחות לקלט אחד יש אפס לוגי, אז הפלט יהיה יחידה לוגית. אותו מצב בפלט יהיה במקרה בו אפסים קיימים בשתי הכניסות בבת אחת. זהו מאפיין חשוב מאוד של אלמנטים AND-NOT: אם אתה מחבר בין שתי הכניסות, אז האלמנט AND-NOT הופך למהפך - הוא פשוט מבצע את הפונקציה של NOT. מאפיין זה מאפשר לך לא לשים שבב מיוחד המכיל שישה ממירים בבת אחת, כאשר נדרש רק אחד או שניים.
שנית, אפס בפלט ניתן להשיג רק אם "אוספים" על כל תשומות האחדות. במקרה זה, יהיה מקום לציין את היסוד הלוגי הנחשב 2I-NOT. השניים אומרים כי אלמנט זה הוא שני קלטים. כמעט בכל סדרות המיקרו-מעגלים ישנם גם אלמנטים של כניסה 3, 4 ושמונה. יתר על כן, לכל אחד מהם יש רק דרך אחת החוצה. עם זאת, האלמנט 2I-NOT נחשב ליסוד בסיסי בסדרות רבות של מעגלי מיקרו דיגיטליים.
עם אפשרויות שונות לחיבור התשומות, תוכלו לקבל נכס נפלא נוסף. לדוגמא, חיבור שלושת הכניסות של אלמנט הכניסה 8I-NOT יחד, נקבל את האלמנט 6I-NOT. ואם אתה מחבר את כל 8 הכניסות יחד, אתה מקבל רק מהפך, כאמור לעיל.
זה משלים את ההיכרות עם האלמנטים ההגיוניים. בחלק הבא של המאמר, נשקול את הניסויים הפשוטים ביותר עם מעגלי מיקרו, את המבנה הפנימי של מעגלי מיקרו, מכשירים פשוטים, כמו גנרטורים לדופק.
בוריס אלאדישקין
המשך המאמר: שבבי היגיון. חלק 3
ראה גם באתר elektrohomepro.com
: