אלגברה בוליאית. חלק 1. קצת היסטוריה

בבית הספר כולנו למדנו אלגברה, אבל לא דיברו שם על אלגברה בוליטית. מה ההבדל בין אלגברה בוליטית לאלגברה בבתי ספר, ההיסטוריה של המראה שלה, בעיות ויישומים מתוארים במאמר זה.

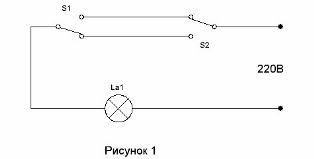
המעגל המאפשר לשני מתגים להדליק את האור במסדרון בכניסה למסדרון ולכבות אותו כשנכנסים לחדר היה ידוע זמן רב מאוד (ראה. מעגל בקרת תאורת פרוזדור) זה מוצג באיור 1.

משימה מספר 1. מסובך יותר. צרו תרשים המאפשר לכם להדליק ולכבות את האור בחדר שלכם עם כל אחד מ -3 מתגים שונים. מתגים ממוקמים בכניסה לחדר, מעל המיטה ובשולחן העבודה.

משימה מספר 2.

בוועדת ספורט, דוגמת ועדת מפעל, התכנסו 5 שופטים.

על כל אחד מהם להצביע לקבלת החלטות שונות. ההחלטה מתקבלת ברוב קולות, אך רק בתנאי הנוסף שיושב ראש הוועדה יצביע בעדה.

השופטים מצביעים בלחיצה על הכפתור שסוגר את המתג שנמצא מתחת לשולחן בו הם יושבים. סוגרים את המתג הם מצביעים בעד ומנתקים את החסרונות. צייר תרשים פשוט המאפשר לך לראות אוטומטית את תוצאות ההצבעה. במקרה הפשוט ביותר, פשוט בעזרת נורה - מוארת - ההחלטה התקבלה, לא נדלקה - לא.

משימה מספר 3. בפועל, זה לא סביר, אך כמשימה חינוכית מורכבת היא די מתאימה.

בחדר משושה גדול מותקן מתג אחד על כל קיר. בנה מעגל כך שבכל עת תוכל להדליק או לכבות את האור בחדר על ידי סיבוב מתג אחד (כל).

לאחר שתשבת ללא הצלחה על משימות במשך שלושה עד ארבעה ימים, הניח אותן בצד באופן זמני. ולהתעסק אלגברה בוליאית. זו אלגברה בוליאנית, או כפי שהיא מכונה גם, אלגברה בוליאנית, אלגברה במעגל ממסר, יעזור לך לפתור את הבעיות שלך.

מה זה אלגברה בוליטית?

באופן מוזר, למרות העובדה שבמשך חמש שנים הם לומדים אלגברה בבית הספר, תלמידים רבים, ומאוחר יותר מבוגרים, לא יוכלו לענות על השאלה, מה זה אלגברה? אלגברה היא מדע הבוחן את התפאורה של כמה אלמנטים ואת הפעולות עליהם.

בקורס בית ספר באלגברה, אלמנטים כאלה הם מספרים. ניתן לציין מספרים לא לפי מספרים, אלא באמצעות אותיות, כולם מכירים את זה. בשיעורים הראשונים של אלגברה, זה תמיד מקשה על תלמידים רבים. זכרו כמה היה קשה בהתחלה להתרגל להוסיף אותיות במקום מספרים, לפתור משוואות שאינן אומרות דבר.

כנראה שכל אחד מאיתנו שאל את עצמנו את השאלה: "מדוע עלינו להזין אותיות במקום מספרים והאם זה בכלל הכרחי?" ורק אחר כך ראית מה היתרונות שמעניקה אלגברה כשאתה פותר בעיות בהשוואה לחשבון.

אלגברה משמשת במדעים מדויקים רבים. זו פיזיקה, מכניקה, סופרומט, חשמל. חוק אוהם אין יותר משוואה אלגברית: מספיק להחליף את הערכים המספריים שלהם במקום אותיות כדי לגלות איזה זרם יזרום בעומס, או איזו התנגדות יש לקטע במעגל.

אז התוודע לאלגברה של מספרים, או לאלגברה אלמנטרית. המשימה העיקרית והכמעט ייחודית היא לקבל תשובה לשאלה: "למה שווה X? כמה? "

בתיכון הם בוחנים את תחילתה של אלגברה וקטורית. אלגברה זו שונה באופן מהותי מאלגברה אלמנטרית. יש לו אופי שונה של הסט הנחקר וכללי פעולה אחרים. בפתרון משוואת הווקטור נקבל בתשובה וקטור שאינו מספר רגיל שעונה על השאלה "כמה?"

הנוסחאות של אלגברה וקטורית שונות במובנים רבים מהנוסחאות של אלגברה אלמנטרית. לדוגמה, באלגברה אלמנטרית ובאלגברה וקטורית יש פעולת תוספת. אבל זה מבוצע בדרכים שונות לחלוטין.תוספת מספרים אינה דומה כלל לתוספת וקטורים.

יש אלגבריות אחרות: אלגברה לינארית, אלגברה של מבנים, אלגברה של טבעות, אלגברה של היגיון, או, מה זהה, אלגברה בוליטית. בטח לא שמעת את השם בשיעורי בית הספר. ג'ורג 'בולי - אבל כולם יודעים את שמה של אחת מבנותיו המוכשרות אתל וויניץ '(1864 - 1960). היא כתבה את הרומן "Gadfly", המדבר על המאבק לזכויותיהם של הפחמלאים האיטלקים.

ג'ורג 'בול נולד באנגליה ב- 2 בנובמבר 1815. כל חייו עבד כמורה למתמטיקה ופיזיקה בבית הספר. מתוך זיכרונותיהם של תלמידיו נודע איזו חשיבות רבה הוסיף בול להתפתחות יכולות היצירה של התלמידים. בהצגת חומר חדש הוא ביקש להבטיח שתלמידיו עצמם "יגלו מחדש" נוסחאות וחוקים מסוימים.

כשהמורה סיפר לסטודנטים על הקשיים שעימם מתמודדים מדענים בהכרח בחיפוש אחר האמת, המורה אהב לחזור על חוכמה מזרחית אחת: אפילו כס המלכות הפרסי לא יכול להביא לאדם כל כך הנאה כמו התגלית המדעית הקטנה ביותר. בוהל מעולם לא איבד תקווה שיום אחד תלמידיו יגלו תגלית אמיתית.

מגוון האינטרסים המדעיים של בוהל היה רחב מאוד: הוא התעניין באותה מידה במתמטיקה והגיון - מדע החוקים וצורות החשיבה. בימים ההם ההיגיון נחשב למדעי מדעי הרוח, ורבים שהכירו את ג'ורג 'בולי התפלאו כיצד שיטות הקוגניציה המדויקות הטמונות במתמטיקה ושיטות לוגיקה תיאוריות בלבד יכלו להתקיים באדם אחד.

אבל המדען רצה להפוך את מדע החוקים וצורות החשיבה לקפדניים כמו כל אחד ממדעי הטבע, אומרים מתמטיקה ופיזיקה. לשם כך, בול התחיל לציין לא מספרים כאותיות, כפי שנעשה באלגברה רגילה, אלא באמירות, והראה כי משוואות כאלה, הדומות מאוד לאלה האלגבריים, יכולות לפתור שאלות לגבי אמיתות וכזביות של הצהרות שהאדם עשה. אז האלגברה הבולית קמה.

אך הרבה לפני שג'ורג 'בוהל, המתמטיקאי והפילוסוף הגרמני גוטפריד לייבניץ (1646-1716) הגה לראשונה את הרעיון ליצור מדע שיציין את כל המושגים של דיבור קולקטיבי רגיל עם סמלים ויציב איזו אלגברה חדשה לשילוב סמלים אלה.

לאחר יצירתו של מדע כזה, על פי לייבניץ, מדענים ופילוסופים יפסיקו להתווכח ולצעוק זה על זה, לגלות את האמת, אך הם יאספו עיפרון ויגידו ברוגע: "בואו נחשב!"

כיום אלגברה של ההיגיון הפכה לחלק חשוב במתמטיקה. אחת ממשימותיה היא לפתור כל מיני משוואות, שיחסיהן המספריים מוחלפים על ידי אלפביתיות. כל אחד מכם, כנראה, לאורך חייכם נזכר כיצד לפתור משוואות של התואר השני והשלישי עם מקדמי אותיות. אז, בולי באלגברה החדשה שלו השתמש בכל הנוסחאות והחוקים הללו.

מה שחדש באלגברה הבולאנית הוא שאלמנטים של הסט שנלמדים בה אינם מספרים, אלא הצהרות. אם כאשר פותרים משוואות אלגבריות רגילות, נקבע איזה מספר שווה ל- X לא ידוע, אלגברה בבית הספר מחפשת את התשובה לשאלה: "כמה?"

אלגברה של ההיגיון מחפשת את התשובה לשאלה: "האם אמירה זו או אחרת שמציינת האות X נכונה?"

משמעות ההצהרה ותוכנה אינם ממלאים שום תפקיד כאן. כל הצהרה יכולה להיות נכונה או שקרית בלבד. זה לא יכול להיות חצי נכון וחצי שקרי. כדוגמא, אנו יכולים לזכור שהשליכו הרבה מטבעות.

רק שתי מצבי מטבע נחשבים שם - ראשים או זנבות. בהסכמת הצדדים, הנשר הוא כן, והזנבות הם לא. לא נלקחות בחשבון נקודות ביניים אחרות בתורת ההסתברות, אף שהן אפשריות. מטבע הפוך יכול ליפול על קצה, להתגלגל במורד הרצפה אל רגלי הכיסא או השולחן ולהישאר במצב זקוף, או אפילו ליפול לפער רחב ברצפה. (באופן אנלוגי למעגלי חשמל, ניתן לשקול את שני המצבים האחרונים כתקלה בצורה של מגע שרוף).אך בימים ההם, אלגברה בוליטית, אבוי, לא הייתה בשימוש נרחב.

קלוד שאנון "גילה" שוב את האלגברה של בוהל. בשנת 1938, בעודו סטודנט במכון הטכנולוגי של מסצ'וסטס ואמריקה, קלוד הצעיר הוכיח כי האלגברה הבוליאנית מתאימה לחלוטין לניתוח ולסינתזה של מעגלי ממסר ומיתוג.

בעזרת האלגברה הבוליאנית קל מאוד ליצור מעגל חשמלי של אוטומט הפועל על ממסר.לשם כך, מסתבר, אתה רק צריך לדעת בדיוק מה המכונה צריכה לעשות, כלומר אתה צריך שיהיה לך אלגוריתם להפעלתה. לכן הונח התשתית לתאוריה של מכונות דיגיטליות הפועלות על פי העיקרון של כן או לא.

כזה, בקצרה, הוא ההיסטוריה של האלגברה הבולאנית. במאמרים שלהלן נשקול את חוקי היסוד שלה, דוגמאות למעגלי קשר המיישמים חוקים אלה. שקול את הפיתרון של המשימות שניתנו בתחילת המאמר.

המשך המאמר: אלגברה בוליאית. חלק 2. חוקים ותפקודים בסיסיים

בוריס אלאדישקין