"הכל זורם", או חוק אוהם לסקרנים

אפילו הלופר האחרון שלמד זמן מה בכיתה י 'יגיד זאת למורה החוק של אוהם - זהו "U שווה ל- I פעמים R". לרוע המזל, התלמיד המצוין והחכם ביותר יגיד מעט יותר - הצד הפיזי של החוק של אוהם יישאר בגדר תעלומה עבור שבעה כלבי ים. אני מרשה לעצמי לשתף עם עמיתי את החוויה שלי בהצגת נושא פרימיטיבי לכאורה זה.

מטרת העשייה הפדגוגית שלי הייתה האמנות וההומניטרית בכיתה י ', שתחומי העניין העיקריים שלה, כפי שהקורא מנחש, היו רחוקים מאוד מהפיזיקה. זו הסיבה שהוראת נושא זה הופקדה בידי מחבר שורות אלה, שבאופן כללי מלמד ביולוגיה. זה היה לפני כמה שנים.

השיעור על חוק אוהם מתחיל באמירה הטריוויאלית כי זרם חשמלי הוא תנועה של חלקיקים טעונים בשדה חשמלי. אם רק כוח חשמלי פועל על חלקיק טעון, החלקיק יואץ בהתאם לחוק השני של ניוטון. ואם הווקטור של הכוח החשמלי הפועל על החלקיק הטעון קבוע על מסלול המסלול כולו, אז הוא מאיץ באותה מידה. ממש כמו שמשקל נופל תחת השפעת כוח הכבידה.

אבל כאן הצנחן צונח לגמרי לגמרי. אם אנו מזניחים את הרוח, אז קצב הנפילה שלה קבוע. אפילו תלמיד הכיתה לאמנות והומניטרית יענה כי בנוסף לכוח הכובד, כוח נופל אחר פועל על המצנח הנופל - כוח ההתנגדות האווירית. כוח זה שווה בערך המוחלט לכוח המשיכה של המצנח על ידי כדור הארץ והוא מנוגד אליו בכיוון. למה? זו שאלת המפתח בשיעור. לאחר דיון מסוים, אנו מגיעים למסקנה שכוח הגרר מתגבר עם גידול בשיעור הנפילה. לפיכך, הגוף הנופל מאיץ למהירות שבה הכבידה והתנגדות האוויר משתוות, והגוף נופל במהירות קבועה.

נכון, במקרה של צנחן המצב מעט מסובך יותר. המצנח לא נפתח מייד והצנחן מאיץ במהירות גבוהה משמעותית. וכשהמצנח כבר נפתח, הנפילה מתחילה בהאטה, שנמשכת עד לאיזון כוח הכובד וכוח ההתנגדות האווירית.

עבור מטען מצנח עם מסה מוחלטת m ​​יורדת במהירות קבועה v, אנו יכולים לכתוב: mg - F (v) = 0, כאשר F (v) הוא כוח התנגדות האוויר, הנחשב כפונקציה של קצב הנפילה. לגבי צורת הפונקציה F (v) אנו יכולים לומר רק דבר אחד עד כה: הוא צומח בצורה מונוטונית. הנסיבות הזו היא שמייצבת מהירות.

במקרה הפשוט ביותר, כאשר F (v) = k, המהירות הקבועה בה ייפול המצנח יהיה שווה ל- mg / k. בואו נעשה קצת המרה עכשיו. תן לצניחה ליפול מגובה h. אז ההבדל באנרגיות הפוטנציאליות של הגוף לפני הנפילה ואחריה יהיה שווה ל- mgh = mU, כאשר U הוא האנרגיה הפוטנציאלית של גוף בעל מסה יחידה בגובה h, או ההבדל הפוטנציאלי של שדה הכבידה בנקודות ההיארעות הראשוניות והסופיות.

לאור האמור לעיל, אנו משיגים את הנוסחה: F (v) = mU / h. (1)

ועכשיו חזרה למוליך דרכו זורם זרם חשמלי. מספר גדול של חלקיקים טעונים נעים לאורך המוליך, המתנגשים באטומים לעתים קרובות יותר ככל שהם עפים מהר יותר. האנלוגיה לירידה של מצנח היא שקופה למדי, ההבדל היחיד הוא שיש הרבה "מצנחים" והם נעים לא בכבידה אלא בשדה החשמלי. בהתחשב בנסיבות אלה, (1) ניתן לכתוב מחדש בצורה: F (v) = eU / l, (2)

כאשר e הוא מטען החלקיקים, U הוא הפרש הפוטנציאל החשמלי בקצות המוליך, אני אורך המוליך.חוזק הזרם ברור שווה ל- I = neS, כאשר n הוא מספר החלקיקים הטעונים לנפח יחידה, S הוא אזור חתך הרוחב של המוליך, הוא מהירות החלקיקים (לשם הפשטות אנו מניחים שכל החלקיקים הטעונים זהים).

כדי להשיג את התלות I (U), עליכם לדעת במפורש את התלות F (). האפשרות הפשוטה ביותר (F = k) מעניקה מייד לחוק של אוהם (I ~ U):

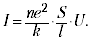
הערך נקרא מוליכות, וההדדיות בו נקראת התנגדות. לכבוד מגלה החוק, ההתנגדות מתבטאת בדרך כלל באוהם.

הערך (ne2 / k) נקרא המוליכות הספציפית, והערך ההפוך שלו נקרא ההתנגדות הספציפית. ערכים אלה מאפיינים את החומר ממנו מורכב המוליך. זה משמעותי כי המוליכות היא פרופורציונאלית למספר החלקיקים הטעונים לנפח יחידה (n). בפתרונות מתכות ואלקטרוליטים המספר הזה גדול, אך בדיאלקטריקה הוא קטן. מספר החלקיקים הטעונים לנפח יחידת גז יכול להיות תלוי בשדה המופעל (כלומר, זהו פונקציה של U), ולכן חוק אוהם אינו חל על גזים.

כשגזרנו את החוק של אוהם, הנחנו הנחה אחת לא ברורה. קיבלנו שהכוח המעכב תנועה של חלקיק טעון הוא פרופורציונאלי למהירותו. כמובן שאפשר לנסות להצדיק איכשהו איכשהו, אך האימות הניסיוני נראה הרבה יותר משכנע.

אימות ניסיוני של הנחה זו הוא, כמובן, אימות של החוק של אוהם עצמו, כלומר המידתיות של U ו- I. נראה שזה לא קשה לעשות: יש לנו מד מתח ומד זרם! אבוי, הכל לא כל כך פשוט. עלינו להסביר לתלמידים שלנו שמד מתח, בדיוק כמו מד זרם, אינו מודד מתח, אלא חוזק זרם. ויש לנו את הזכות לקבוע וולט בסולם המתח רק בגלל שאנחנו מכירים בתחילה את החוק של אוהם, אותו אנו רוצים לבדוק. זקוקים לגישות אחרות.

אתה יכול, למשל, להשתמש ברעיון הבא. אנו מחברים סוללות n בסדרות ומניחים שהמתח במקרה זה גדל פי n. אם החוק של אוהם נכון, אז החוזק הנוכחי יגדל גם פי n, שבגללו היחס n / I (n) לא יהיה תלוי ב- n. הנחה זו מוצדקת על ידי ניסיון. נכון, לסוללות יש גם התנגדות פנימית, וזו הסיבה שערך n / I (n) גדל לאט עם הגדלת ה- n, אך לא קשה לתקן זאת. (ג 'אוהם עצמו נמדד לחץ בצורה שונה, שתלמידים יכולים לקרוא עליהם בספר הלימוד של G.Ya. Myakishev ואחרים.)

אנו שואלים את השאלה: "" בקונסטלציה הרחוקה של טאו סטי ", לא החוק של אוהם, אלא החוק של המדען המקומי הגדול אקדמי X. על פי חוק X, חוזק הזרם פרופורציונלי לריבוע ההפרש הפוטנציאלי בקצות המוליך. איך כוח הבלימה של חלקיקים תלוי במהירותם בטאו סטי? " בעזרת טרנספורמציות פשוטות מגיעים התלמידים למסקנה שהכוח פרופורציונאלי לשורש המהירות של הריבוע.

ועכשיו נעבור לתהליך אחר: תנועת מים בצינור שבקצותיהם נוצרים לחצים שונים. כאן יש לנו מצב שונה לחלוטין: לא חלקיקים נעים אינדיבידואליים משפשפים על גבי חומר נייח המופץ על כל נפח המוליך, אלא שכבות של חלקיקים נעים משפשפים זה בזה. ונסיבה זו משנה באופן מהותי את כל ההנמקות הגופניות.

שני כוחות פועלים על שכבה נפרדת של מים הנעים בצינור:

א) ההבדל בכוחות הלחץ בקצות השכבה;

ב) כוח החיכוך נגד שכבות מים שכנות.

אם נקבעת מהירות קבועה של השכבה, אז כוחות אלה שווים ומכוונים לכיוונים מנוגדים.

כוח החיכוך כנגד שכבות מים שכנות יכול להאט את התנועה אם ורק אם שכבות מים שונות נעות במהירויות שונות. במוליך, מהירות החלקיקים הטעונים אינה תלויה אם הם בקצה המוליך או במרכזו, אך המים במרכז הצינור נעים במהירות, ולאט לאט לאורך הקצוות, ממש על פני הצינור, מהירות המים היא אפס.

אנלוגי של חוזק הנוכחי יכול להיחשב כזרם מים, כלומר כמות המים הזורמת מהצינור לזמן יחידה. מכיוון שמהירות המים בשכבות שונות אינה זהה, חישוב קצב הזרימה אינו כה פשוט.אנלוגי להבדל בפוטנציאלים חשמליים הוא הפרש הלחץ בקצוות הצינור.

ממש כמו במוליך עם זרם, מידתיות ישירה נצפית בצינור עם מים בין הפרש הלחץ בקצוות וקצב הזרימה. אך מקדם המידתיות שונה לחלוטין. ראשית, קצב זרימת המים תלוי לא רק בשטח חתך הצינור, אלא גם בצורתם. אם הצינור גלילי, אז קצב הזרימה הוא ביחס ישר לא שטח החתך, אלא לריבוע שלו (כלומר, הרדיוס לתואר הרביעי). תלות זו מכונה חוק פויסויל.

זה הזמן לזכור את מהלך האנטומיה, הפיזיולוגיה וההיגיינה, שנלמד בכיתה ט '. בגוף האדם יש מספר גדול של כלים המחוברים במקביל. נניח שאחת מכלים אלה התרחבה, והרדיוס שלה התגבר מעט, רק הוכפל. כמה פעמים, עם אותו לחץ בקצות הכלי, תגדל כמות הדם העוברת בו? שטח החתך הוא פרופורציונלי לריבוע הרדיוס, וריבוע שטח החתך פרופורציונאלי לרדיוס מדרגה רביעית. לכן, כאשר מכפילים את הרדיוס, זרימת הדם עולה 16 (!) פעמים. כזה הוא כוחו של חוק Poiseuille, המאפשר לייצר מנגנון יעיל מאוד להפצה מחדש של הדם בין איברים. אם אלקטרונים לא היו זורמים בכלי דם, הזרימה שלהם הייתה גדלה רק ארבע פעמים.

התיאור של הנושא שתואר לעיל שונה מזה המסורתי. ראשית, מושקעים שלושה שיעורים בנושא, אשר עם המחסור הנוכחי של שעות, יכול להיחשב כמותרות בלתי קבילות למדעי הטבע. עם זאת, הדבר מוצדק מהעובדה שניתן לחשוף בפשטות ופופולרית למדי את המשמעות הפיזית של החוק ולצייד את התלמידים במתודולוגיה בה הם יכולים להשתמש כדי לנתח מגוון תהליכים פיזיים: נפילת גוף באוויר, תנועת נוזל בצינור, תנועה של חלקיקים טעונים לאורך מוליך, ובהמשך בניתוח מעבר זרם חשמלי דרך ואקום ובאמצעות גזים.

גישה זו נקראת שילוב בין-תחומי. בעזרתו הדגמנו בפני התלמידים תכונות נפוצות במבט ראשון רחוק, בקטעי הפיזיקה, הראינו שהפיזיקה אינה "חבורה" של "חוקים פיזיים" שאינם קשורים זה בזה, אלא בניין דק. כך גם כמובן לגבי תחומים מדעיים אחרים. וכך, נראה, בזבוז לא הגיוני של שעות ההדרכה משתלם לחלוטין.

קרא גם:כיצד להשתמש במולטימטר