קטגוריות: מאמרים מוצגים » אלקטרוניקה מעשית
מספר צפיות: 32001
הערות לכתבה: 2
קבלים במעגלים אלקטרוניים
במאמרים קודמים דיברנו בקצרה על פעולת קבלים במעגלי זרם חילופין, כיצד ומדוע קבלים מעבירים זרם זרם חילופין (ראה - קבלים AC) במקרה זה הקבלים אינם מתחממים, הכוח לא מוקצה להם: במחצית הגל האחד של הסינוסואיד, הקבלים נטענים, ובאחר, הוא באופן טבעי פורק, תוך העברת האנרגיה המאוחסנת חזרה למקור הנוכחי.
שיטה זו של העברת זרם מאפשרת לקרוא לקבל התנגדות חופשית, וזו הסיבה שהקבל המחובר לשקע אינו גורם לסיבוב הדלפק. וכל זה נובע מכך שהזרם בקבל מקדים בדיוק את 1/4 מהזמן שהמתח המופעל עליו.
אולם התקדמות שלב זו מאפשרת לא רק "להערים" על הדלפק, אלא גם מאפשרת ליצור מעגלים שונים, למשל, גנרטורים של אותות סינוסים ומלבניים, עיכובי זמן ומסנני תדרים שונים.
בתהליך של סיפור זה יהיה צורך לזכור לפעמים את מה שכבר נאמר בעבר, כביכול, לסיכום. זה יעזור לא לחזור למאמרים קודמים כדי לזכור נוסחה פשוטה, או בפשטות, "מה זה?"
חיבור מקבילי וסדרה של קבלים
עם חיבור מקביל של קבלים, הקיבולת הכוללת היא פשוט הסכום האריתמטי של הקיבולות. באופן טבעי, עם הכללה זו הקיבול הכולל יהיה גדול יותר מהקיבול של הקבל הגדול ביותר. Cototal = C1 + C2 + C3 + ... + Cn.
במקרה של חיבור סדרה, הקיבולת הכוללת פחותה מזו של הקטן ביותר.
1 / Ctotal = 1 / C1 + 1 / C2 + 1 / C3 + ... + 1 / Cn.
כאשר שני קבלים זהים מחוברים בסדרה, הקיבול הכולל יהיה שווה למחצית הקיבול של אחד: לדוגמה, בעת חיבור שני קבלים של 1 μF כל אחד, הקיבול הכולל יהיה 0.5 μF.
קיבול Xc
כאן, הכל, כמו בחיבור נגדים, הוא רק ההפך הגמור: חיבור סדרתי מקטין את הקיבול הכולל, בעוד שקבילה מקבילה מגדילה אותו. אין לשכוח נסיבות אלה בעת חיבור קבלים, שכן עלייה בקיבול מובילה לירידה בקיבול Xc
Xc = 1/2 * π * f * C.
מבחינת המתמטיקה, זה די טבעי, מכיוון שהיכולת C היא במכנה של השבר. אגב, התדר f נמצא באותו מקום, ולכן עלייה בתדר מביאה גם לירידה בקיבולת Xc. המשמעות הפיזית של זה היא שבאמצעות אותו קבל עדיף, ללא הפרעה, שיעברו תדרים גבוהים. זה יידון מעט בהמשך, כשמדובר במסנני הנמוך והעברה.
אם ניקח קבל עם הספק של 1 מיקרומטר, אז לתדר של 60 הרץ ה- Xc שלו יהיה 2653 אוהם, ולתדר של 400 הרץ לאותו קבל יש Xc של 398 אוהם בלבד. מי שרוצה יכול לבדוק תוצאות אלו על ידי הנוסחה, תוך החלפת π = 3.14, התדר בהרץ, והקיבול בפאראדים. ואז התוצאה תהיה באוהם. הכל חייב לעמוד במערכת SI!
אבל קבלים משמשים לא רק כהתנגדות דעיכה חופשית או במסנני מיישר. ללא השתתפותם, מעגלים לגנרטורים בתדרים נמוכים וגבוהים, ממירי צורת גל שונים, מבדילים ומשלבים מעגלים, מגברים ותכניות אחרות.
בשלב הבא, ישקול אותות חשמליים שונים שקבלנים צריכים לעבוד איתם. ראשית כל, מדובר באותות תקופתיים המתאימים לתצפית עם אוסצילוסקופ.
תקופת התנודות ותדירותן
תנודה תקופתית נקראת אפוא תקופתית, אשר ללא הפסקה חוזרת על אותה צורה, למשל, תנודת סינוסואידית אחת. משך התנופה המלאה נקרא בדיוק התקופה T, ונמדד בשניות, אלפיות השנייה, מיקרו-שניות.האלקטרוניקה המודרנית אפילו עוסקת בננו-שניות (מיליארדית השנייה).
מספר התקופות בשנייה נקרא התדר (באיזו תדירות) של התנודות f, ומתבטא בהרץ. 1 הרץ הוא התדר בו מתנדנד תנודה אחת, תקופה שלמה, תוך שנייה אחת. היחס בין התקופה לתדר מתבטא בנוסחה הפשוטה T = 1 / f.
בהתאם, בידיעת תקופת התנודה, פשוט מאוד לחשב את התדר f = 1 / T.
כך מחושב התדר כאשר מודדים בעזרת אוסילוסקופ: מספר התאים בתקופה מחושב, כפול משך התא אחד, והתקופה מתקבלת, למשל, במיקרו-שניות. וכדי לברר את התדירות, הם פשוט השתמשו בנוסחה האחרונה.
רגיל אוסצילוסקופ אלקטרוני מאפשרת לצפות רק באותות תקופתיים הניתנים לסנכרון עם תדירות הגלישה על מנת לקבל תמונת סטילס המתאימה למחקר. אם אתה שולח אות לתוכנית מוסיקה לכניסת האוסילוסקופ, לא תוכל לעצור את התמונה בשום דבר. כדי לצפות באותות כאלה משתמשים באוסילוסקופים לאחסון.
כאשר נמדדת תקופה באלפיות השנייה, התדר מתקבל בקילוהרץ, לתקופה שנמדדת במיקרו-שניות, התדר כבר מתבטא במגה-הרץ. זה אם אתה לא עומד בדרישות מערכת SI: תקופה בשניות, תדר בהרץ.
רעידות לא סינוסואליות
כאמור, גל סינוס הוא הנפוץ ביותר ומתאים ללימוד ושימוש מעשי בעקומה התקופתית. בתנאים תעשייתיים הוא מתקבל באמצעות גנרטורים חשמליים, למשל, בתחנות כוח הידרואלקטריות. במכשירים אלקטרוניים משתמשים בתנודות עם הצורות השונות ביותר.
בעיקרון, מדובר בשלוש צורות: סינוסואידלי, מלבני ומשולש, כפי שמוצג באיור 1. גם זרם ומתח יכולים להיות בעלי צורה כזו, לפיכך, הדמות מציגה רק את ציר הזמן, ציר הסדר נותר ללא שם.
תנודות כאלה נוצרות על ידי מעגלים אלקטרוניים מיוחדים. אותות מלבניים ומשולשים נקראים לרוב פולסים. עם זאת, ישנם המון מעגלים אלקטרוניים המבצעים המרת אות: לדוגמא מלבן, משולש ניתן ליצור מסינוסואיד.
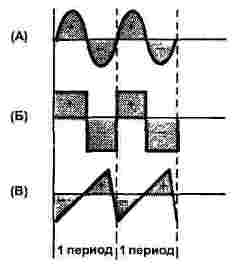
איור 1
עבור כל שלושת האותות, האיור מציג שתי תקופות, לכל האותות יש אותו תדר.
ספקטרום של אותות לא סינוסים
ניתן לייצג כל אות חשמלי כמדידת המשרעת בנקודה מסוימת בזמן. התדר של דגימות אלה נקרא תדר הדגימה, וגדול לפחות פעמיים מהתדר העליון של האות שנמדד. ואז מדגימות אלה תוכלו לשחזר את האות המקורי. שיטה זו משמשת למשל בהקלטת סאונד דיגיטלי. שיטה זו נקראת גם ניתוח זמן.
שיטה אחרת מניחה שאפשר לייצג כל אות, אפילו מלבני, כסכום האלגברי של סינוסואידים עם תדרים ושלבים שונים. שיטה זו נקראת ניתוח תדרים. אולם מה שנאמר "עם תדרים שונים" אינו נכון לחלוטין: הסינוסואידים המרכיבים נקראים הרמוניות והתדרים שלהם מצייתים לחוקים מסוימים.
גל סינוס שתדרו שווה לתדר של גל מרובע נקרא הרמוני המהותי או הראשון. אפילו הרמוניות מתקבלות על ידי הכפלת התדר הבסיסי במספר שווה, והרמוניות משונות, בהתאמה, על ידי אי-זוגיות.
לפיכך, אם להרמוני הראשון יש תדר של 1000 הרץ, אז השני הוא 2000 הרץ, הרביעי הוא 4000 הרץ וכו '. להרמוניה משונה יהיו תדרים של 3000 הרץ, 5000 הרץ. יתרה מזאת, כל הרמוני קטן יותר במשרעת מאשר העיקרי: ככל שההרמוני גבוה יותר, כך המשרעת קטנה יותר.
במוזיקה, הרמוניות נקראות גוון יתר. הם אלה שיוצרים את קטע הצליל, מאפשרים להבדיל בין הכינור לפסנתר, והגיטרה מהסקסופון. הם לא מאפשרים לבלבל את הקול הגברי והנקבי או להבדיל בין פטרוב לאיבנוב. ורק הסינוסואיד עצמו כבר לא ניתן לפרק או להרכיב מכל אות.
איור 2 מראה את הבנייה של דופק מלבני.
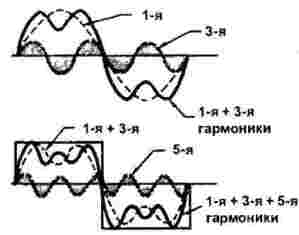
איור 2
ההרמוניות הראשונות והשלישיות מוצגות בחלק העליון של הדמות. קל לראות שבתקופה אחת משלוש התקופות ההרמוניות הראשונות של המעבר השלישי. במקרה זה, המשרעת של ההרמוני השלישי היא שליש מהראשונה. סכום ההרמוניות הראשונה והשלישית מוצג גם כאן.
להלן, יחד עם סכום ההרמוניות 1 ו -3, מוצגים עוד 5 הרמוניות: לתקופה של אות מלבני הוא מצליח לבצע חמש תקופות בדיוק. במקרה זה, המשרעת שלו קטנה עוד יותר, ליתר דיוק, בדיוק 1/5 מהאחת העיקרית (הראשונה). אך אין לחשוב שהכל מסתיים בהרמוניה החמישית: פשוט אי אפשר להראות באיור, למעשה יש הרבה יותר.
היווצרות אותות מסור ומשולש, המוצגים באיור 3, מורכבים מעט יותר. אם במקרה הקודם רק הרמוניות משונות השתתפו, אז אפילו הרמוניות נכנסות לפעולה.
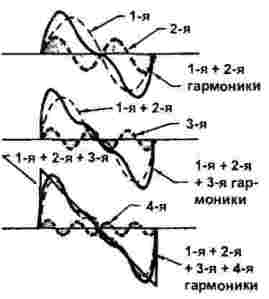
איור 3
לפיכך, אנו יכולים לקבוע את העובדה שבעזרת הרמוניות רבות מסונתז איתות בכל צורה, ומספר ההרמוניות תלויות בצורת הגל, כמוצג באיורים 2 ו -3.
בעת תיקון והתקנת ציוד אלקטרוני משתמשים באוסילוסקופ לחקר אותות חשמליים. זה מאפשר לך לשקול את צורת האותות התקופתיים, את המשרעת שלהם, למדוד את תקופת החזרה. אך לא ניתן לראות את ההרמוניות המוצגות בתמונות 2 ו -3.
גם אם אתה מחבר, למשל, גיטרה חשמלית לאוסילוסקופ, משוך מיתר אחד, סינוסואיד מופיע על המסך, זה הרמוני הראשון. במקרה זה, לא ניתן לדבר על שום גוון יתר. אותו סינוסואיד יגרום אם תנפצו בצינור או בחליל מול המיקרופון.
כיצד להשיג דחפים מלבניים
לאחר היכרות עם אותות חשמליים, עלינו לזכור את קבלים איתם החל המאמר. ראשית, כדאי שתכירו את אחד ממעגלי האלקטרוניקה הקלאסיים - מולטיברטור, (איור 4) הוא זה שמייצר פולסים מלבניים. המעגל כל כך קלאסי שהוא מתחיל לעבוד מייד מבלי לדרוש הגדרות או התאמות.
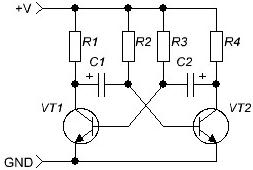
איור 4
המולטיברטור הוא מגבר דו-שלבי, המכוסה על ידי משוב חיובי. אם נגדי עומס האספנים R1 = R4, נגדי הבסיס R2 = R3 והקבלים C1 = C2 שווים, המולטיברטור נקרא סימטרי ומייצר פולסים של גל מרובע מסוג הברזל - משך הדופק שווה למשך ההשהיה.
מחזור התפקיד של פולסים כאלה (היחס בין התקופה למשך הדופק) שווה לשניים. בסכמות בשפה האנגלית הכל בדיוק הפוך: הם מכנים זאת מחזור חובה. זה מחושב כיחס בין משך הדופק לתקופת הירושה שלו ובא לידי ביטוי כאחוז. לפיכך, עבור המתפתל, מחזור החובה הוא 50%.
האם המחשב נכון?
השם multivibrator הוצע על ידי הפיזיקאי ההולנדי ואן דר פול, מכיוון שהספקטרום של אות מלבני מכיל הרמוניות רבות. אתה יכול לאמת זאת אם אתה יכול להציב מקלט רדיו הפועל בטווח הגלים הבינוני ליד מולטיברטור שעובד אפילו בתדר שמע: יללות יבואו מהרמקול. זה מרמז כי בנוסף לתדר הקול, המולטיברטור פולט גם תנודות בתדר גבוה.
כדי לקבוע את תדירות הייצור, ניתן להשתמש בנוסחה f = 700 / (C1 * R2).
עם צורה זו של הנוסחה, הקיבול של הקבל במיקרו-פארדות (μF), ההתנגדות בקילו-אוהם (KΩ), התוצאה בהרץ (הרץ). לפיכך, התדר נקבע על ידי קבוע הזמן של מעגל C1 * R2; עומסי אספן אינם משפיעים על התדר. אם ניקח C1 = 0.02 μF, R2 = 39 KΩ, נקבל f = 700 / (0.02 * 39) = 897.4 הרץ.
מולטיברטור בעידן המחשבים בקרי מיקרו על פי תכנית זו כמעט אף פעם לא משתמשים בה, אם כי יתכן שהיא מתאימה לניסויים שונים. קודם כל, שימוש במחשבים. כך נראה מעגל המולטיברטור המורכב בתוכנית Multisim. החיבור של האוסילוסקופ מוצג גם כאן.
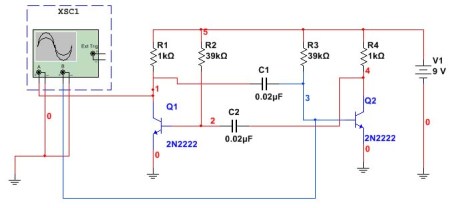
איור 5
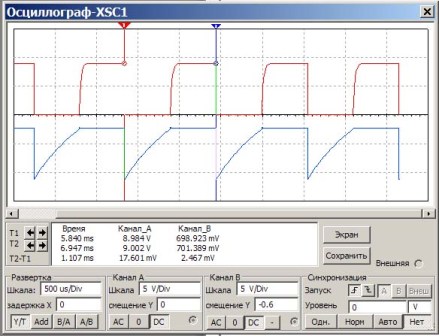
במעגל זה מותקנים קבלים ונגדים כמו בדוגמה הקודמת. המשימה היא לבדוק את החישוב לפי הנוסחה אם יתקבל אותו תדר. לשם כך, מודדים את פרק הזמן של הקטניות ואז מחשבים אותם מחדש בתדירות. התוצאה של אוסצילוסקופ Multisim מוצגת באיור 6.
איור 6
כמה הבהרות לתרשים 6.
על גבי מסך האוסילוסקופ הדופק האדום מראה את הפולסים על אספן הטרנזיסטורים ואת הכחול בבסיסים. מתחת למסך בחלון לבן גדול, המספרים מראים את תוצאות המדידה. אנו מעוניינים בעמודה "זמן". הזמן נמדד על ידי אינדיקטורים T1 ו- T2 (משולשים אדומים וכחולים מעל המסך).
כך, תקופת החזרת הדופק T2-T1 = 1.107ms מוצגת די מדויקת. נותר רק לחשב את התדר f = 1 / T = 1 / 1,107 * 1000 = 903Hz.
התוצאה כמעט זהה לחישוב לפי הנוסחה הניתנת מעט גבוהה יותר.
ניתן להשתמש בקבלים לא רק בנפרד: בשילוב עם נגדים, הם מאפשרים לכם פשוט ליצור פילטרים שונים או ליצור מעגלי מעבר-פאזות. אך על כך נדון במאמר הבא.
המשך המאמר: קבלים במעגלים אלקטרוניים. חלק ב '
בוריס אלאדישקין
ראה גם באתר elektrohomepro.com
: