מה הקשר בין קטעי התיל לאוכלוסיית הארנבונים?

בשנת 1202, המתמטיקאי האיטלקי לאונרדו פיבונצ'י פרסם את עבודתו תחת הכותרת "ספר אבקוס" ("ספר החישובים"), בו תיאר גם את סדרות המספרים שהונצחו בשמו. באחד הפרקים מנסה פיבונאצ'י להראות באופן מתמטי כיצד יגדל מספר הארנבים. הוא ראה בהשערות הבאות כתנאים:

1) בחודשיים הראשונים זוג ארנבונים לא נותנים צאצאים;

2) החל מהחודש השלישי זוג ארנבים נותן זוג ארנבים נוסף.

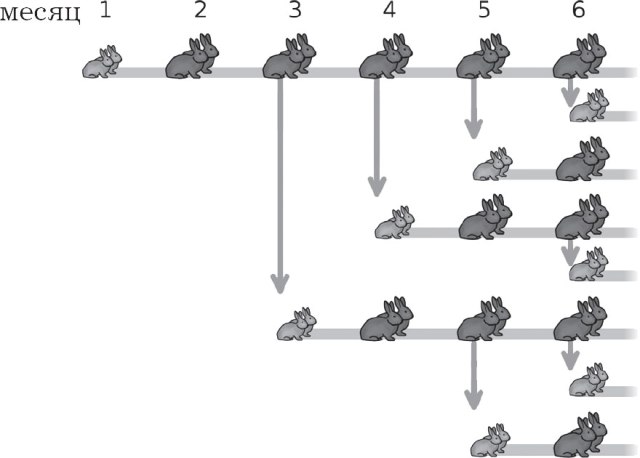
כתוצאה מבניית דפוס גידול של אוכלוסיית הארנבונים, אנו משיגים את סדרת המספרים הבאה, תוך ציון העלייה במספר הארנבים מדי חודש:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 …

1 + 1 = 2; 1 + 2 = 3; 2 + 3 = 5; 3 + 5 = 8…

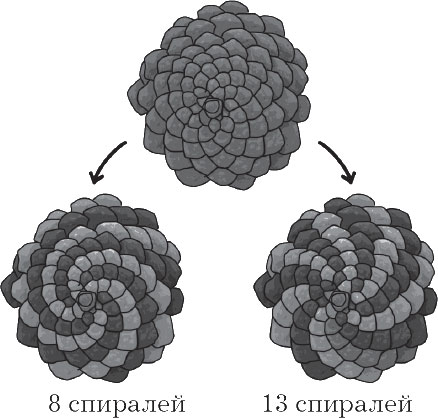
אם תסתכל בקפידה על הגבשושיות, תראה שהמשטח שלה מורכב מאזניים המעוותים בספירלה בהתאם לרצף פיבונאצ'י. בעודם באננס או בפרח חמנית, הם נראים לעין בלתי מזוינת.

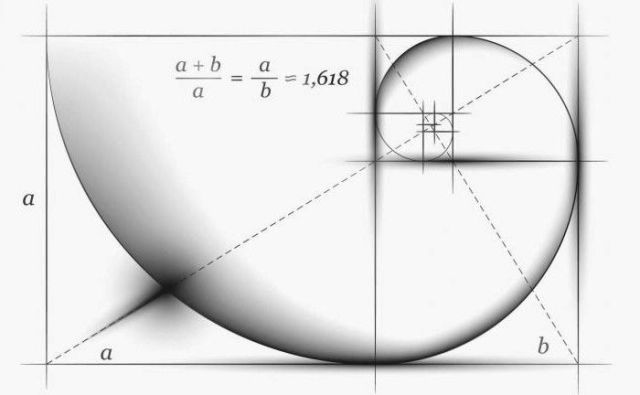
מאז ימי קדם יחס הזהב, המספר = 1.618. היוונים הקדמונים שקלו בערך הפרופורציה האידיאלית. יחס הזהב הוא היחס של כל מספר עוקב אחרון בסדרת פיבונאצ'י לזה הקודם:

144/89=89/55=55/34=34/21=21/13=13/8=8/5=5/3=1,618...

היוונים הקדמונים השתמשו בזה בארכיטקטורה. לחזית הפרתנון באתונה פרופורציות דומות מאוד עם מלבן הבנוי על עיקרון יחס הזהב.

אז מה היופי ברצף קטעי החוט, הזרמים המדורגים של זרמי חשמל וניתוק מפסקי חשמל? בנה סדרה של מספרים עם הערכים הבאים: 1,5; 2.5; 4; 6; 10; 16; 25; 40; 63...

זרמים מדורגים של מתחילים אלקטרומגנטיים:

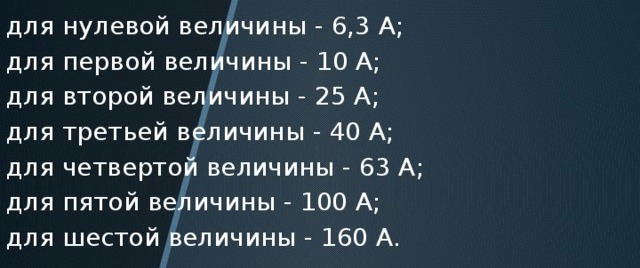
אז אם אתה מחלק 2.5 / 1.5; 4 / 2.5; 6.3 / 4; 10 / 6.3; 16/10; 25/16; 40/25; 63/40ואז יש לנו בערך 1.6. התואם לכלל יחס הזהב. ומשקף את היופי והגאונות של הטבע אפילו במערכות ההנדסיות המשעממות שלנו.

מה אתה חושב? האם זו תאונה?

מבוסס על הספר "רומן נהדר על מתמטיקה. תולדות העולם דרך הפריזמה של המתמטיקה" מאת מייקל לון. תודה על ההמלצה של ולדימיר קיסל.

אלכסיי בושניאגה